5.4 역행렬
선형 변환을 수행하는 행렬은 본질적으로 함수의 성질을 지니기 때문에 항등함수와 역함수에 대응하는 항등행렬Identity matrix, 역행렬 Inverse matrix 이 존재함
*항등행렬 Identity matrix
원공간의 변화없이 동일한 공간으로 유지하는 변환
$$I=\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix}$$
*역행렬 Inverse matrix
행렬 곱의 결과가 항등행렬이 나오는 행렬
$A\cdot A^-1 = A^-1\cdot A =1$
5.4.1 역행렬의 존재를 판별하는 행렬식
어떤 함수가 역함수를 갖기위한 조건이 전단사 함수이듯이 행렬도 전단사로 대응되어야 한다.
어떤 행렬에 대해 역행렬이 조재하는 지 파악할 수 있는 수식을 행렬식 Dterminant 이라 한다.
det() 로 표시한다.
$$A=\begin{bmatrix}a & b \\c & d \end{bmatrix}$$
$det(A)=ad-bc$

변환된 두 벡터가 이루는 면적의 넓이는 $det(A)=ad-bc$ 로 구할 수 있다.
| $Area(P)$ | $= (a+b)\cdot (c\cdot d)-2 \cdot (\frac{1}{2} ac)-2\cdot (\frac{1}{2} bd)-vc-bc $ |
| $=(a+b)\cdot (c+d)-ac-bd-2bc$ | |
| $=ad-bc$ |
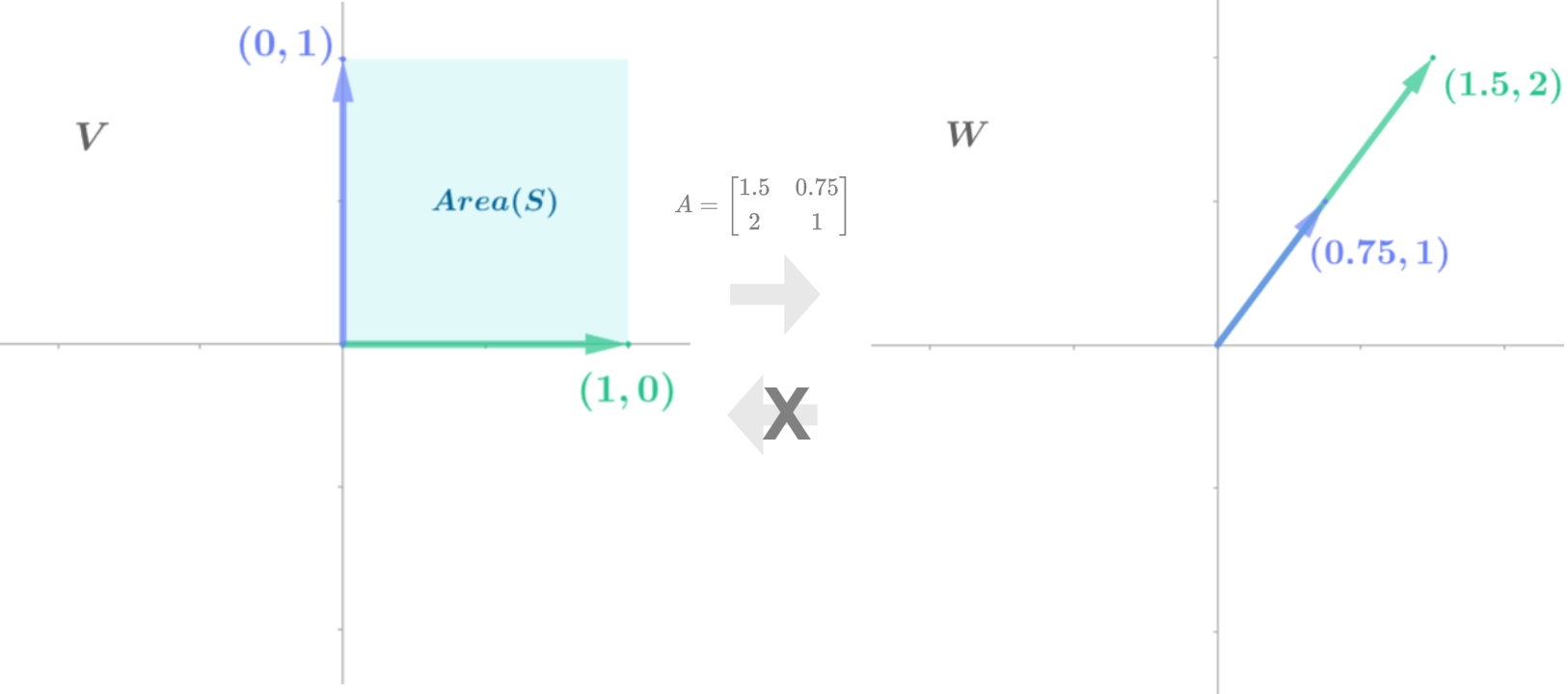
이 행렬식이 0일 경우 2차원 평면 영역이 1차원 직선 영역으로 압축된것과 같기 때문에 역행렬이 존재할 수 없다.

행렬식의 계산결과 부호에 따라 원 공간과 동일한 면인지 뒤집힌 반대면인지 파악할 수 있다.
5.4.2 크기 변환행렬의 역행렬
a,b에 역수를 대입해 구할 수 있다.
| $$S= \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} $$ | $$S^{-1}=\begin{bmatrix} \frac {1}{a} & 0 \\ 0 & \frac {1}{b} \end{bmatrix}$$ |
5.4.3 전단 변환행렬의 역행렬
a에 반대수를 대입
| $$S= \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} $$ | $$S= \begin{bmatrix} 1 & -a \\ 0 & 1 \end{bmatrix} $$ |
5.4.4 회전 변환행렬의 역행렬
회전각 $\theta$ 에 대한 반대방향의 회전각 $-\theta$에 대한 회전 변환을 의미한다.
$$R^{-1}_\theta =R_{(-\theta)}$$
회전행렬의 역행렬은 다음과 같으며 서로 전치 관계에 있음을 알 수 있다.
| $$R_\theta = \begin{bmatrix}cos\theta & -sin \theta \\ sin\theta & cos \theta \end{bmatrix}$$ | $$R^{-1}_\theta = \begin{bmatrix}cos\theta & sin \theta \\ -sin\theta & cos \theta \end{bmatrix}$$ |
$R^{-1}_\theta = R^T_{\theta}$
* 삼각함수의 성질
$cos(-\theta )= cos( \theta )$
: 코사인 함수의 짝수 함수 성질 $ f(−x)=f(x) $
$sin( -\theta ) =-sin( \theta )$
: 사인함수의 홀수 함수 성질 $ f(−x)=−f(x) $
5.4.5 행렬 곱의 역행렬
합성함수의 역함수와 같이 역행렬도 동일하게 다음의 수식이 성립한다.
$(A\cdot B) ^{-1} =A^{-1}\cdot B^{-1}$
'study > math' 카테고리의 다른 글
| [이득우 게임수학] 선그리기 알고리즘 (0) | 2024.07.05 |
|---|---|
| [이득우 게임수학] 아핀공간 (0) | 2024.07.03 |
| [이득우 게임수학] 행렬의 설계 (0) | 2024.06.26 |
| [이득우 게임수학] 행렬 (0) | 2024.06.17 |
| [이득우 게임수학] 선형성과 선형변환 (0) | 2024.06.09 |




댓글