[이득우 게임수학] 아핀공간

https://blog.naver.com/ideugu/221409774016

크기, 회전, 밀기 선형 변환은 행렬 곱으로 표현이 가능하지만 이동변환은  $2\times 2$ 정방행렬 곱셈으로는 구현이 불가능하기 떄문에 행렬곱으로 표현하기 위해 아핀 공간이 필요하다.

6.1 아핀공간

이동 변환은 $2\times 2$ 정방행렬 곱셈으로는 구현이 불가능하다.

기저벡터가 원점에서 출발해야 한다는 조건을 만족하지 못하기 떄문.

임의의 베벡터 (x,y)를 지정 크기(a,b)만큼 이동시키는 기능
$$\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}x+a\\ y+b\end{array}\right]$$	$$A\cdot \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}x+a\\ y+b\end{array}\right]$$
행렬의 덧셈	? 존재하지 않음

 

행렬이 되기 위해서는 선형성 (기저벡터가 원점에서 출발하는 조건)을 만족해야하지만 이동변환은 그럴 수 없다.

전단변환

 

전단 변환은 표전기저벡터 $e_1$을 고정시킨 상태에서 옆으로 밀어 공간을 기울이는데

이러한 전단변환을 성질을 이용하면 특정 조건하에 이동기능 구현이 가능하다.

$$S=\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]$$

 

 

$$\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ 1\end{array}\right]=\left[\begin{array}{c}x+a\\ 1\end{array}\right]$$

y=1인 조건하에 a 만큼 미는 전단변환의 결과는 1차원의 이동변환 x+a 로 활용 할 수 있다.

z축 추가

이를 2차원으로 적용한다면 3차원으로 공간을 확장하여 마지막차원인 z  값을 1로 고정한 조건으로 전단 변환을 설계할 수 있다.

$$\left[\begin{array}{ccc}1& 0& a\\ 0& 1& b\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+a\\ y+b\\ 1\end{array}\right]$$

이를 이동 변환행렬 이라고 한다.

$$T=\left[\begin{array}{ccc}1& 0& a\\ 0& 1& b\\ 0& 0& 1\end{array}\right]$$

이렇게 한차원 높여 설계한 선형변환을 아핀변환 Affine transformation 이라고 한다.

크기변환 (S)	$$\left[\begin{array}{ccc}a& 0& 0\\ 0& b& 0\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}ax\\ by\\ 1\end{array}\right]$$
회전변환 (R)	$$\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}cos\theta x-sin\theta y\\ sin\theta x+cos\theta y\\ 1\end{array}\right]$$
이동변환 (T)	$$\left[\begin{array}{ccc}1& 0& a\\ 0& 1& b\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+a\\ y+b\\ 1\end{array}\right]$$

 

* 이동 구현하기

 

6.2 아핀공간 구성 요소

점 (Point) 

• 마지막 차원 값이 1인 아핀공간의 원소
• 행렬곱을 사용해 이동이 가능하려면 물체는 점으로 구성되어야함
  2차원 공간의 점 : $(x,y,1)$
  3차원 공간의 점 :  $(x,y,z,1)$

 

* 마지막 차원이 1이 아닌경우?

사용할 수 없음

 

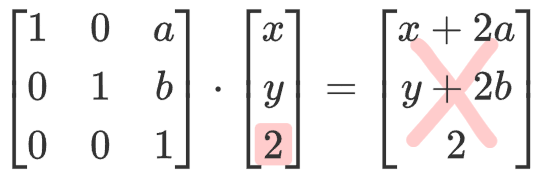
이동벡터 , 변위 벡터 (Displaycement vector)

• 아핀공간 내의 이동을 지정하기 위해 사용된다.
• 벡터공간의 원소와는 다른용도로 사용 → 이동벡터, 변위벡터라 부름
• 점과 점 간의 최단거리로 정의된다.
• 점 $P_1$의 좌표를 $(x_1,y_1,1)$, 점 $P_2$의 좌표를 $(x_2,y_2,1)$로 지정하여 두 점을 뺴서 만든 이동 벡터의 마지막 차원값은  항상 0이 된다.
  $(x_1-x_2,y_1-y_2,0)$ 
  이동 벡터들이 모이면 마지막 차원 z값은 항상 0인 영역을 형성한다. 

6.2 아핀공간 성질

아핀공간의 원점은  (0,0,1)이고 아핀공간속 임의의 점 $P$의 값을 $(x,y,1)$ 로 지정했을때 원점$O$에서 $P$로 향하는 이동벡터 $\vec v$는 다음과 같다.

$\vec v = P-O=(x,y,1)-(0,0,1)= (x,y,0)$

이를 이용하면 점을 이동시킨 결과를 만들어낼 수 있으며 점과 벡터는 다음과 같은 연산 규칙이 있다.

• 점-점 = 벡터
• 점+벡터 = 점
• 벡터+벡터 =벡터
• 점+점 != 점

6.3 아핀 결합

아핀공간 에서 점 끼리의 덧셈은 사용할수 없지만 선형 결합의 결과 마지막 차원의 값이 1을 유지한다면 점과 점을 결합해 새로운 점을 만들 수 있다. 

점 $P_1$  $(x_1,y_1,1)$, 점 $P_2$ $(x_2,y_2,1)$에 각자 스칼라 a,b를 곱한 수식

$a\cdot P_1+b \cdot P_2= ( ax_1+bx_2,ay_1+by_2,a+b )$

$a+b=1$이 되어야한다.

동일한 원리로 여러개의 점을 결합해 새로운 점을 생성하는 수식을 아핀결합 이라고 하며 다음과같이 수식으로 표현한다.

$$\sum _{i=1}^n{c}_i\cdot P_i$$

- n개의 점을 아핀결합하는 경우, 각 점을 $P_i$ - 점에 사용하는 스칼라를 $c_i$로 지정 - 모든 항을 더하는 시그마$\sum$ 기호를 사용

6.3.1 두 점의 결합

두 점을 아핀결합해 새로운 점을 생성하는 경우.

$P_1 ,P_2$로 지정하고 $b$ 를 $(1-a)$로 치환하면 다음 수식이 성립하며 이는 언제나 점의 생성이 보장된다.

$a\cdot P_1+(1-a)\cdot P_2=P'$

이 수식을 사용하여 a 에 값을 대입하면 a의 값이 양으로 커질수록 $P_1$에 가까워지고 음의 방향으로 커질수록 $P_2$에 가까워진다.

이 규칙을 시각화 하면 $P_1 ,P_2$을 지나는 무한한 긴 선이 만들어진다.

이를 수식으로 묶어 정리하면 아래와 같은 식이 성립된다.

 

$a(P_1-P_2)= (P'-P_2)$
$P_1-P_2$	$(P'-P_2)$
$P_2$에서 $P_1$으로 향하는 벡터	$P_2$에서 $P'$으로 향하는 벡터
$a\cdot$ $\vec u$ $=$ $\vec v$

스칼라곱 특성상 $\vec u$와$\vec v$는 서로 평행한 벡터이며, 그렇기 떄문에 두 점의 아핀 결합으로 생성되는 점은  $P_1 ,P_2$을 지나는 직선상에 위치함을 알 수 있다.

 

a에 모든 실수를 대입하면 두점을 이은 무한한 선을 얻을 수 있으며 이  수식을 직선의 방정식이라고 한다.

$L(a) =a\cdot P_1+(1-a)\cdot P_2$

 

* a의 범위에 따라 대응되는 직선의 종류

직선 Line	반직선 Ray	선분 Line segment
$-\infty <a<\infty$	$0 \leq a <\infty$	$0 \leq a \leq1$
두점의 양쪽 방향으로 무한이 뻗어나가는 선의 형태	지정 위치에서 한쪽 방향으로만 뻗어나가는 선 레이케스팅에 활용 Raytracing	시작과 끝이 정해져있는 선