5.3 행렬의 설계
벡터공간$V$의 두 기저벡터가 선형 변환을 통해 $W$ 의 벡터 $(a,c)$와 $(b,d)$ 에 대응되어 변환되는 상황 가정
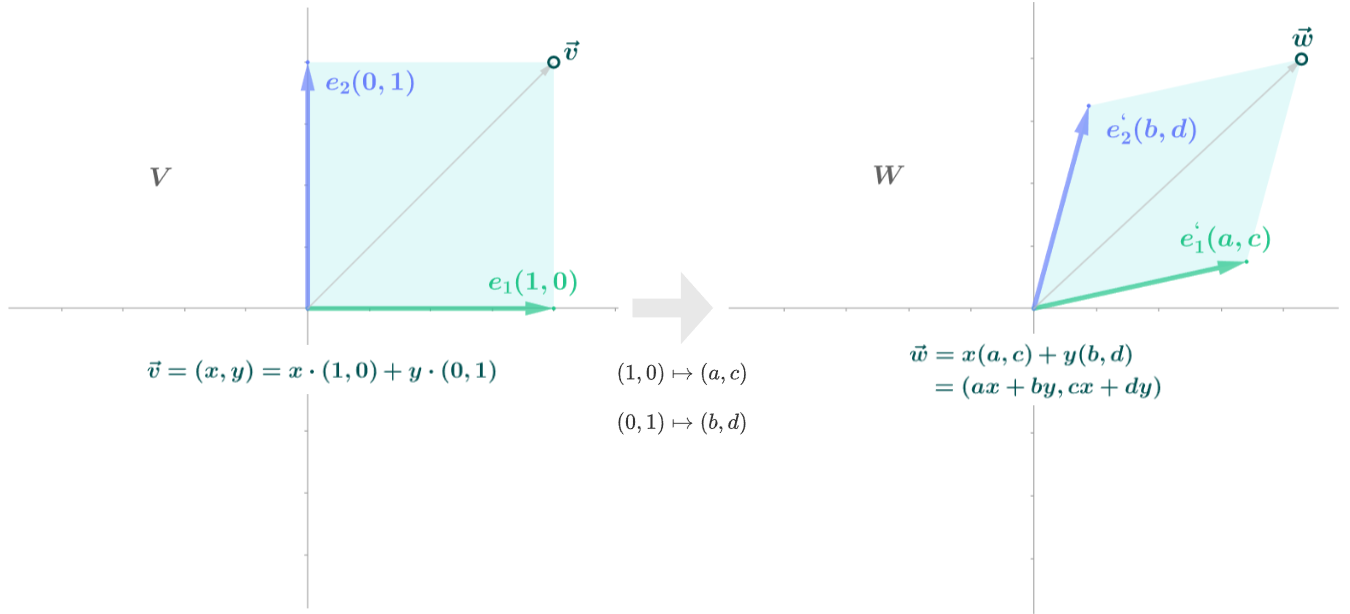
| $\vec v=(x,y) =x\cdot (1,0) + y\cdot (0,1)$ | $\vec w =x(a,c)+y(b,d) =(ax+by,cx+dy)$ |
| 정방향렬에 벡터(x,y)를 곱한것과 동일 $$\begin{bmatrix}a & b \\c & d \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}$$ |
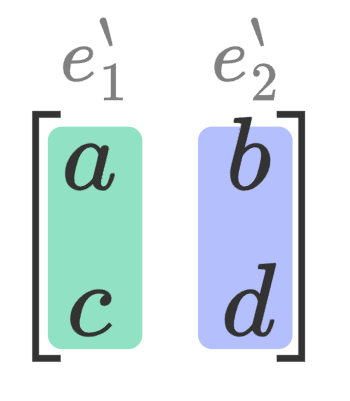
$(a,c) (b,d)$는 정방행렬을 구성하는 열벡터임을 알수 있다.
5.3.1 크기 변환행렬
물체의 크기를 변경하는 행렬은 각 표준 기저벡터를 동일한 방향으로 지정한 크기만큼 늘리는 변환을 의미한다.
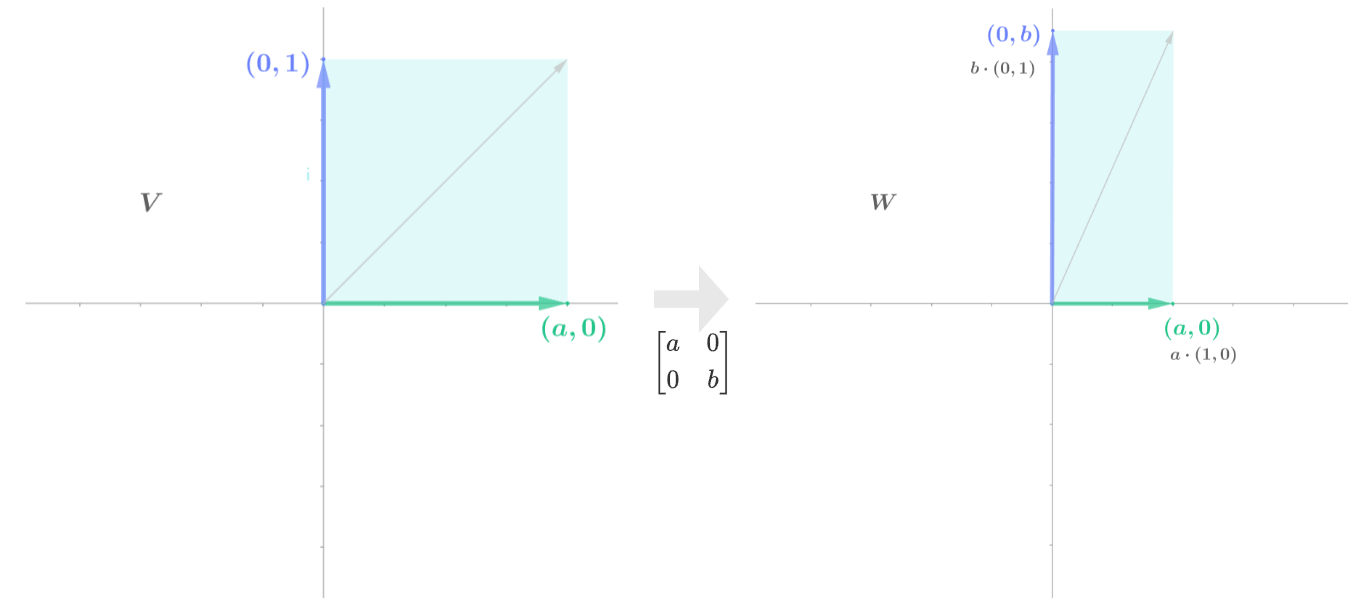
$e_1$를 a 배 늘린 벡터 : $a\cdot (1,0) =(a,0)$
$e_2$를 b 배 늘린 벡터 : $b\cdot (0,1) =(0,b)$
두 표준기저벡터(a,0)과 (0,b)를 열벡터로 설정해 생성한 크기변환 행렬은 다음과 같다
$$S=\begin{bmatrix}a & 0 \\0 & b \end{bmatrix}$$
5.3.2 회전 변환행렬
두 표준 기저벡터가 각$\theta$만큼 회전한 결과는 각각 $( cos\theta , -sin \theta)$ , $( sin \theta, cos \theta)$ 이다.

삼각함수 포스팅 : https://8trian8.tistory.com/93
따라서 각 $\theta$ 에 대한 회전 변환 향렬은 다음과 같다.
$$R_\theta = \begin{bmatrix}cos\theta & -sin \theta \\ sin\theta & cos \theta \end{bmatrix}$$
5.3.3 전단 변환행렬
표준기저벡터 $e_1$을 고정한 상태에서 $e_2$를 x 축방향으로 미는 방식을 전단 변환 행렬이라고 한다.

전단 변환에서 미는 크기는 1행 2열에 위치한 원소 값을 변경해 조절이 가능하다.
$$S=\begin{bmatrix}1 & a \\0 & 1 \end{bmatrix}$$
* 삼각함수의 덧셈정리
$\cos(\alpha + \beta) = \cos\alpha \cos\beta - \sin\alpha \sin\beta$
$\sin(\alpha - \beta) = \sin\alpha \cos\beta - \cos\alpha \sin\beta $

회전변환에 사용하는 두 각 $\alpha$와$\beta$ 가 있을때 이 둘을 합한 $\alpha+\beta$만큼 회전한 변환은 두 각에 대한 회전 변환을 순서대로 적용한 결과와 동일하다.
$$R_{(\alpha+\beta)}=\begin{bmatrix} \cos(\alpha + \beta) & -\sin(\alpha + \beta) \\ \sin(\alpha + \beta) & \cos(\alpha + \beta) \end{bmatrix}$$
또한 각 $\alpha+\beta$ 의 회전변환은 $\alpha$를 수행 한 후 $\beta$에 대한 회전변환을 이어서 한것과 동일하다
$$ R_\alpha \cdot R_\beta = \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix} \begin{bmatrix} \cos \beta & -\sin \beta \\ \sin \beta & \cos \beta \end{bmatrix} $$
$$= \begin{bmatrix} \cos \alpha \cos \beta - \sin \alpha \sin \beta & -\cos \alpha \sin \beta - \sin \alpha \cos \beta \\ \sin \alpha \cos \beta + \cos \alpha \sin \beta & -\sin \alpha \sin \beta + \cos \alpha \cos \beta \end{bmatrix} $$
$$=\begin{bmatrix} \cos(\alpha + \beta) & -\sin(\alpha + \beta) \\ \sin(\alpha + \beta) & \cos(\alpha + \beta) \end{bmatrix}$$
* 전단행렬, 회전변환, 크기변환 행렬 적용해보기

'study > math' 카테고리의 다른 글
| [이득우 게임수학] 아핀공간 (0) | 2024.07.03 |
|---|---|
| [이득우 게임수학] 역행렬 (0) | 2024.06.30 |
| [이득우 게임수학] 행렬 (0) | 2024.06.17 |
| [이득우 게임수학] 선형성과 선형변환 (0) | 2024.06.09 |
| [이득우 게임수학] 삼각함수 (0) | 2024.05.24 |




댓글