[이득우 게임수학] 행렬

https://ko.khanacademy.org/math/precalculus/x9e81a4f98389efdf:matrices/x9e81a4f98389efdf:multiplying-matrices-by-matrices/v/matrix-multiplication-intro

5.2 행렬

행렬은 수를 사각형의 형태로 행과 열을 맞춰 배열한 테이블이다.

2 x 3 행렬은 다음과 같이 2행 3열의 형태이다.

$$\left[\begin{array}{ccc}a& b& c\\ d& e& f\end{array}\right]$$

행렬에서 2차원 백터는 열백터와 행벡터로 표현된다.

열벡터	행벡터
$$A=\left[\begin{array}{cc}x& y\end{array}\right]$$	$$B=\left[\begin{array}{c}x\\ y\end{array}\right]$$

 

정방행렬은 행과 열이 크기가 같은 행렬이다.

선형 변환은 정방행렬을 사용한다. 선형함수 𝑓(𝑥,𝑦)=(𝑎𝑥+𝑏𝑦,𝑐𝑥+𝑑𝑦) 에 대응하는 행렬은 다음과 같다.

 

선형함수 𝑓(𝑥,𝑦)=(𝑎𝑥+𝑏𝑦,𝑐𝑥+𝑑𝑦) 에 대응하는 행렬	A 를 행벡터와 열벡터로 분석
$$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$$	첫번째 행벡터 $A_{row1}$ 은 (a,b) 두번째 행벡터 $A_{row2}$ 은 (c,d) 첫번째 열벡터 $A_{col1}$ 은 (a,c) 두번째 열벡터 $A_{col2}$ 은 (b,d)

 

행렬과 행렬의 덧셈

행렬의 크기가 같은 경우에만 성립된다.

같은 위치의 원소끼리 더한다.

$$A+B=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]+\left[\begin{array}{cc}e& f\\ g& h\end{array}\right]=\left[\begin{array}{cc}a+e& b+f\\ c+g& d+h\end{array}\right]$$

 

행렬과 스칼라 곱셈

행렬의 모든 원소에 스칼라를 곱한다.

$$k\cdot A=k\cdot \left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=\left[\begin{array}{cc}k\cdot a& k\cdot b\\ k\cdot c& k\cdot d\end{array}\right]$$

 

행렬의 전치 (Transpose of a matrix)

첨자 T 로 표시한다.

행과 열을 바꾸는 작업

$${\left[\begin{array}{cc}a& d\\ b& e\\ c& f\end{array}\right]}^T=\left[\begin{array}{ccc}a& b& c\\ d& e& f\end{array}\right]$$ 

정방행렬의 전치 연산은 대각 정보는 그대로 유지되고 나머지 원소가 대각 성분을 중심으로 대칭된 행렬을 만듬

$${\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]}^T=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$$ 

 

행렬과 행렬의 곱셈

행렬의 곱셈은 앞에 위치한 행렬의 행벡터아 뒤에 위치한 행렬의 열벡터를 각각 곱하는 방식으로 진행된다.

행렬 곱셈의 성질
교환법칙이 성립하지 않는다	$A\cdot B \neq B \cdot A$
결합법칙을 만족한다	$(A\cdot B)\cdot C = A \cdot{B \cdot C}$
분배법칙을 만족한다	$A(B+C)=AB+AC$ $(B+C)A=BA+CA$
전치한 결과는 순서를 바꾼 후 각각 전치한 곱과 결과가 동일하다	$(A\cdot B)^T= B^T \cdot A^T$
0의 곱셈성질	$0\cdot A=0$ , $A\cdot 0=0$
차원의 성질	첫 번째 행렬의 열의 개수가 두 번째 행렬의 행의 개수와 동일해야 한다. $m \cdot n$ 행렬과 $n \cdot k$ 행렬의 곱은 $m\cdot k$ 행렬이다.

 

2차원 벡터의 선형변환 행렬

a b c d  네개로 구성된 2x2 정방행렬과 2차원 벡터(x,y)를 열벡터로 설정한 두 행렬의 곱은 선형변환 $f(x,y)=(ax+by,cx+dy)$와 동일하다

a b c d  네개로 구성된 2x2 정방행렬은 2차원 공간의 선형변환에 대응되는 함수를 의미한다.

벡터에 선형 변환을 적용하기 위한 연산 순서는 오른쪽에서 왼쪽 방향으로 이뤄짐을 알 수 있다.

 

벡터$\vec v$ 에 선형 변환을 나타내는 정방행렬 A,B 를 순서대로 연산하여 벡터 $\vec v$ 가 $\vec w$로 변환되는 과정은 다음 행렬곱으로 표현 할 수 있다.

$B \cdot A \cdot \vec v$

 

$$\overrightarrow{w}=\left[\begin{array}{cc}e& f\\ g& h\end{array}\right]\cdot \left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\end{array}\right]$$

 

$$\overrightarrow{w}=B\cdot (A\cdot \overrightarrow{v})=(B\cdot A)\cdot \overrightarrow{v}$$

* 행렬곱 결합법칙 

행렬곱은 결합법칙을 만족하는데 이는 그래픽 연산에서 계산량을 크게 줄이는 역할을 하여 유용하게 활용된다.

 

점이 100개인 물체가 렌더링되기까지 5번의 선형변환이 발생한다고 했을때 행렬곱을 이용한다면 결합법칙으로 인해 계산량을 줄일 수 있다.

 

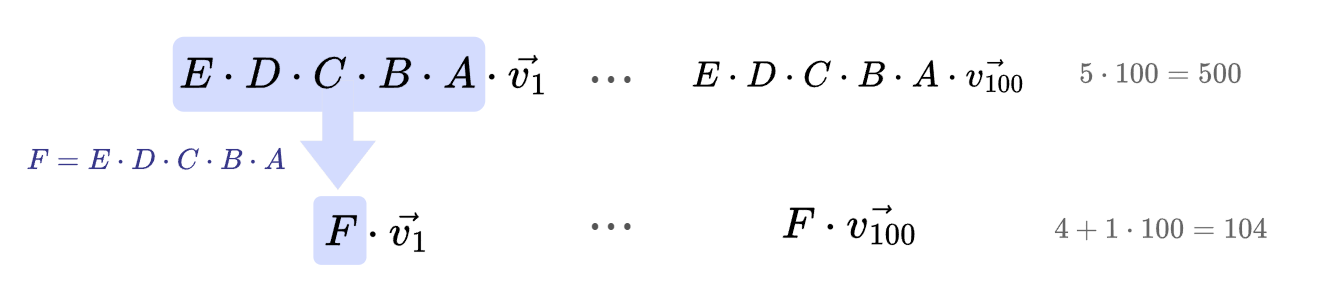
* 열기준 행렬, 행기준 행렬

 

수학에서 행렬을 다룰때는 벡터를 열벡터로 나태내는 열 기준 행렬 방식을 주로 사용하지만 컴퓨터에서는 행기준 행렬을 사용하는 경우가 있다.

이때는 벡터의 위치를 거꾸로 뒤집어 계산해야 행렬의 곱셈이 성립된다.

열기준 행렬	행기준 행렬
$$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}ax+by\\ cx+dy\end{array}\right]$$	$$\left[\begin{array}{cc}x& y\end{array}\right]\cdot \left[\begin{array}{cc}a& c\\ b& d\end{array}\right]=\left[\begin{array}{cc}ax+by& cx+dy\end{array}\right]$$
OpenGL , Unity C#	DirectX ,  Unreal C++

 

열벡터와 행벡터는 서로 전치관계에 있기때문에 선형 변환 역시 전치 관계의 차이만 있다.

$$(A\cdot \overrightarrow{v}{)}^T={\overrightarrow{v}}^T\cdot A^T$$

$$(\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\end{array}\right]{)}^T={\left[\begin{array}{cc}x& y\end{array}\right]}^T\cdot {\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]}^T$$