4.1 삼각함수

$\theta$ : 한 각이 직각인 삼각형에서 밑변과 빗변의 사이각
삼각비 : 직각삼각형을 구성하는 세 변에서 두 변을 뽑아 각각의 비례관계를 나타낸것
| 사인 Sine | $sin (\theta)$ = $a \over c$ |
| 코사인 Cosine | $cos (\theta)$ = $b \over c$ |
| 탄젠트 Tangent | $tan (\theta)$ = $a \over b$ |
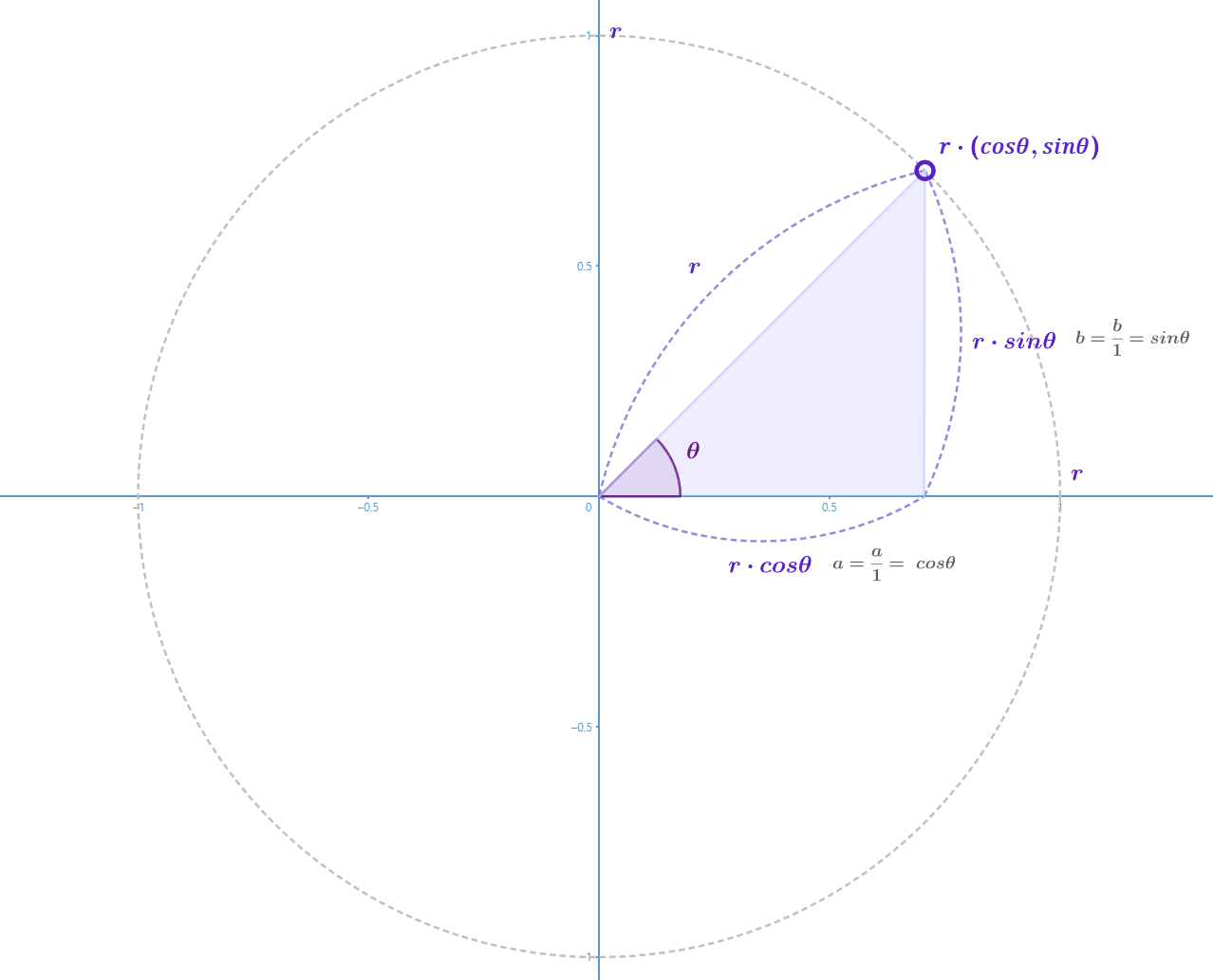
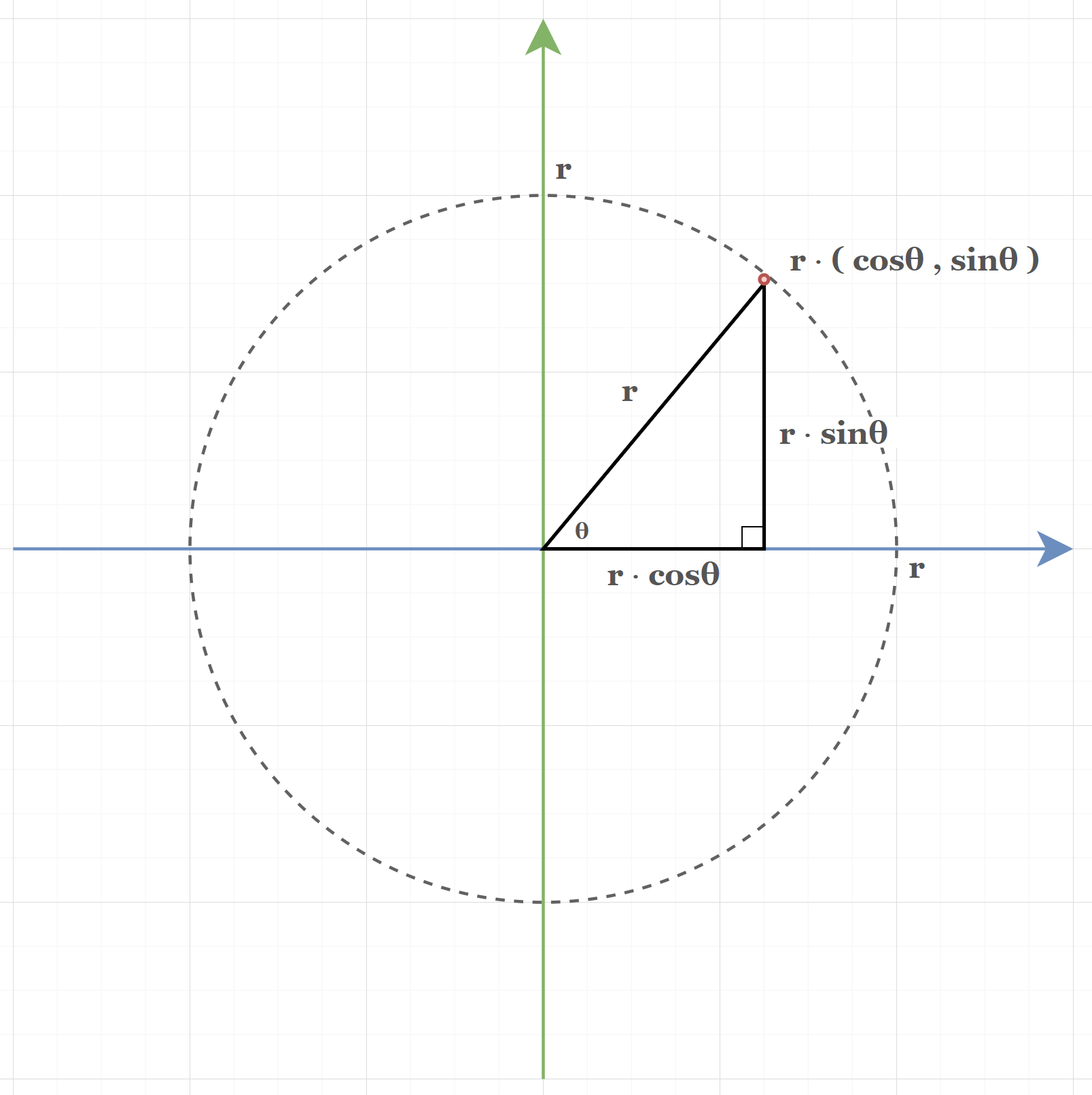
단위 원 (지름 1) 에서의 삼각비를 계산했을때 빗변이 가르키 원의 좌표는 ($cos \theta$,$sin \theta$) 가 됨
$sin \theta ={ b \over 1} =b$
$cos \theta ={ a \over 1} =a$
지름이 r 이라고 했을때 $r\cdot$( $cos \theta$ , $sin \theta$ )
이를 피타고라스 정리에 대입하면 아래와 같은 결과를 얻을 수 있따.
$r^2 (cos^2\theta + sin^2\theta) = r^2$
$cos^2\theta + sin^2\theta = 1$
4.1.1 삼각함수의 성질
Sin , Cos 함수
데카르트 좌표계에서 각도 $\theta$ 는 x 축에서 원의 궤적을 따라 반시계 방향으로 회전한 크기를 의미한다.
각도 0에 대한 sin 함수와 cos 함수의 값은 다음과 같다.
$(cos 0 ^\circ , sin 0 ^\circ) = (1,0)$
각도에 따른 x 값과 y 값의 변화는 -1,1 범위 내에서 $360 ^\circ$ 마다 반복되는데 아래와 같은 패턴을 볼 수 있다.
변화 값의 범위를 진폭, 반복되는 각도를 주기 라고 한다.

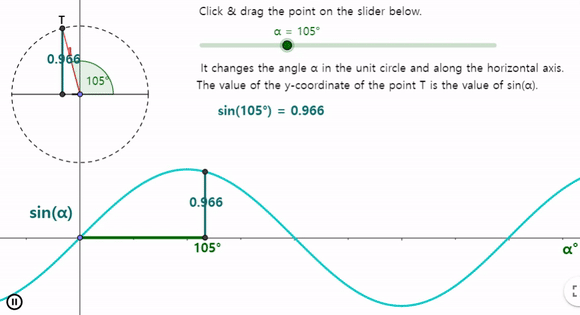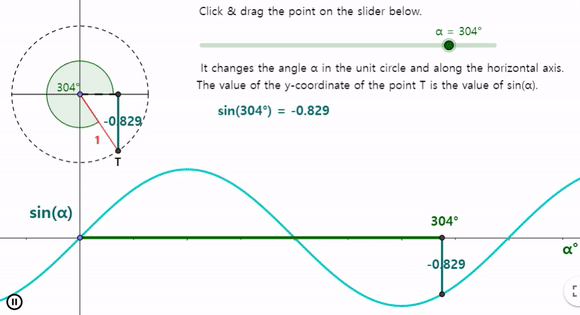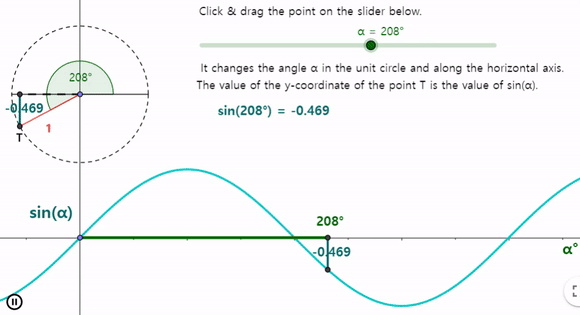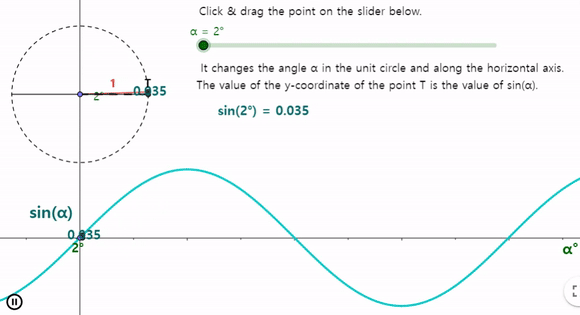

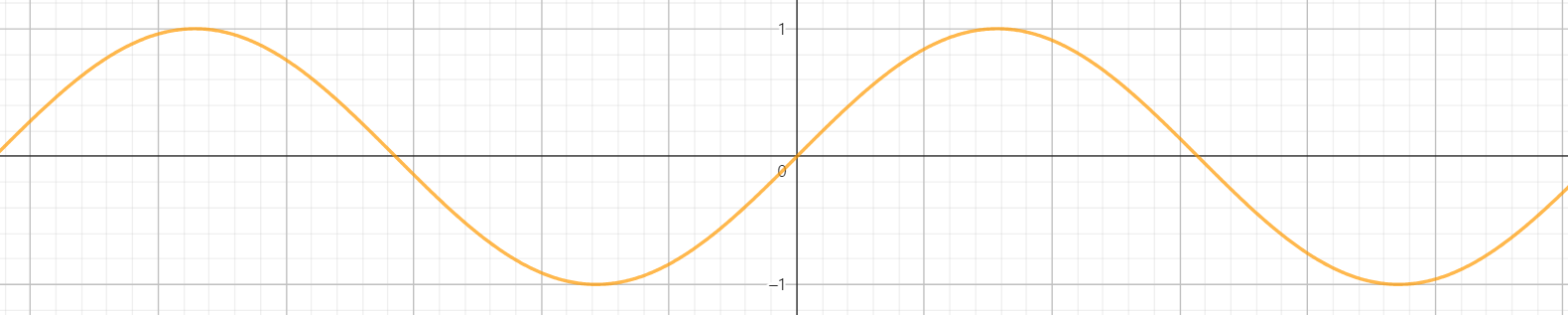
sin 함수와 cos 함수는 한상 -1 에서 1 사이를 일정하게 반복하는 패턴을 띄며 $360 ^\circ$ 주기로 반복되는것을 알수 있다.
cos 함수의 그래프는 좌우대칭 → 짝함수 또는 우함수 → $cos(-\theta) = cos(\theta)$
sin 함수의 그래프 원점 대칭 → 홀함수 또는 기함수 → $sin(-\theta) = -sin(\theta)$
Tan 함수
탄젠트 함수는 빗변과 무관하며 밑변과 높이의 관계를 나타낸다.
tan $\theta$ =$a \over b$ = $\frac{sin\theta}{cos\theta}$
분모의 값이 0이 될수 없기때문에 분모의 값이 0 이되는 $90^\circ$, $270^\circ$ 구간에서의 tan 값은 존재하지 않음.
그래프가 원점 대칭이기때문에 홀함수의 성질을 지녔다.


4.1.2 각의 측정법 : 호도법
각도법(Degree) : 약수가 많은 360을 활용하여 각(Angle)의 크기를 재는 방법. (수가 너무큼)

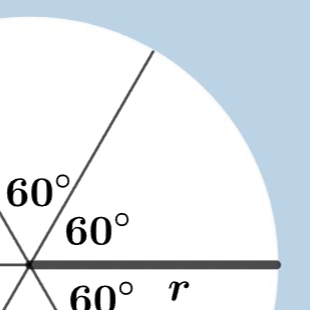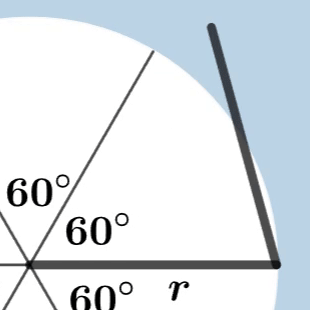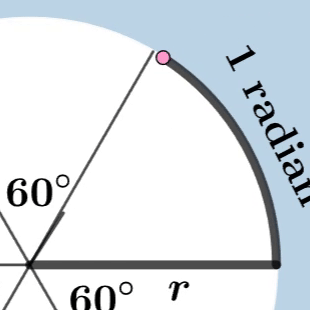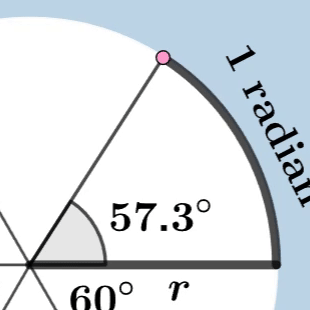
호도법(Radian) : 호의 길이를 기준으로 각을 측정하는 방법
호의 길이와 반지름의 길이가 같은 부채꼴의 중심각
$180^\circ$ 도에 해당하는 반원의 호의 길이는 3.14.. 원주율인 파이($\pi$) 이다.
호의 길이가 반지름인 부채꼴의 각을 1라디안 이라고 하며 각도로 환산하면 $57.2958..^\circ$ 이 된다.
$180^\circ$ 도에 해당하는 반원의 각을 라디안으로 표현하면 ?
$\pi$ = 반원의 호 이기 떄문에 각은 라디안을 기준으로 $\pi$배만큼 크다.
$\pi(rad)= 180^\circ$
$1^\circ = {\pi \over 180} (rad)$
$1(rad) = {(180\over \pi)}^\circ$
4.1.3 삼각함수로 하트 그리기
$ x = 16sin^3\theta$
$y=13cos(\theta)-5cos(2\theta )-2cos(3\theta )-cos(4\theta)$

4.2 물체 회전
기저벡터를 활용해보자
표준 기저벡터 (1,0) $e_1'$ 를 $\theta$만큼 회전한 좌표는 $e_1' = (cos\theta,sin\theta)$ 가 된다.
표준 기저벡터 (0,1) $e_2'$ 를 $\theta$만큼 회전한 좌표는 $e_2' = (-sin\theta,sin\theta)$ 가 된다.
y값만큼의 음의x 값, x값만큼 양의 y값을 가짐.

실 벡터공간의 벡터가 각 $\theta$만큼 회전한것을 선형결합으로 표시하면 $\vec v =1\cdot e_1+1\cdot e_2$ 이다.
이를 치환하면 $\vec v =1\cdot ( cos \theta - sin \theta )+1\cdot ( sin \theta + cos \theta )$
좌표(1,1)이 $\theta$ 만큼 회전한 벡터 $\vec{v}$ 의 좌표는 아래와 같다.
$\vec v = (cos \theta - sin \theta , sin \theta + cos \theta)$
$x' = x cos \theta - y sin \theta $
$y'= x sin \theta + y cos \theta)$

θ = π/4
c = Curve( (16sin(t)^3 * cos(θ) - (13cos(t) - 5cos(2t) - 2cos(3t) - cos(4t)) * sin(θ)), (16sin(t)^3 * sin(θ) + (13cos(t) - 5cos(2t) - 2cos(3t) - cos(4t)) * cos(θ)), t, 0, 2pi )
p = Sequence((16sin(t)^3, 13cos(t) - 5cos(2t) - 2cos(3t) - cos(4t)), t, 0, 2pi, dt)
Polygon(p)https://ko.khanacademy.org/computing/pixar/sets/rotation/v/sets-9
4.3 삼각함수의 역함수
주어진 벡터의 좌표로 부터 이에 대응하는 각도를 구하기 위해서는 삼각함수의 역함수의 성질을 알아야한다.
역함수를 만들기위해서는 정의역과 공역의 범위를 한정시켜 역함수가 존재할수 있는 전단사함수로 만들어야된다.

sin 함수는 정의역의 범위를 -90$^\circ$, 90 $^\circ$ 구간으로 한정하고 공역의 범위를 -1, 1 로 만든다면 sin x 값이 주어졌을때 역함수 가 존재하게 되는데, 이렇게 범위를 제한시켜 얻은 sin 함수의 역함수를 arcsin 함수라고 부른다.
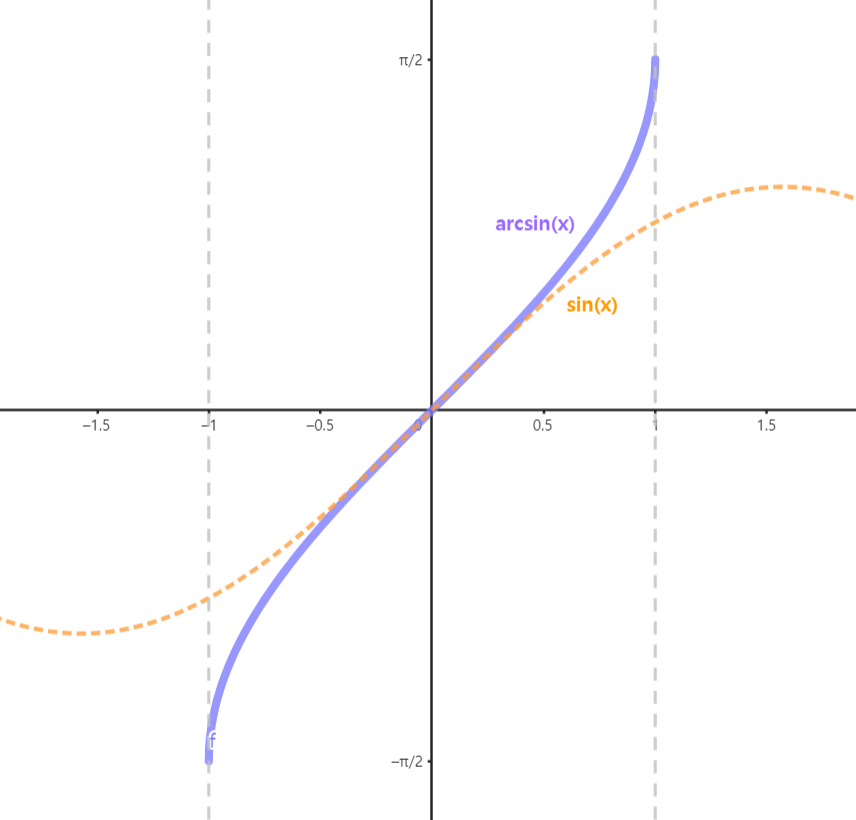
$f^-1= sin^-1(x)=arcsin(x)$
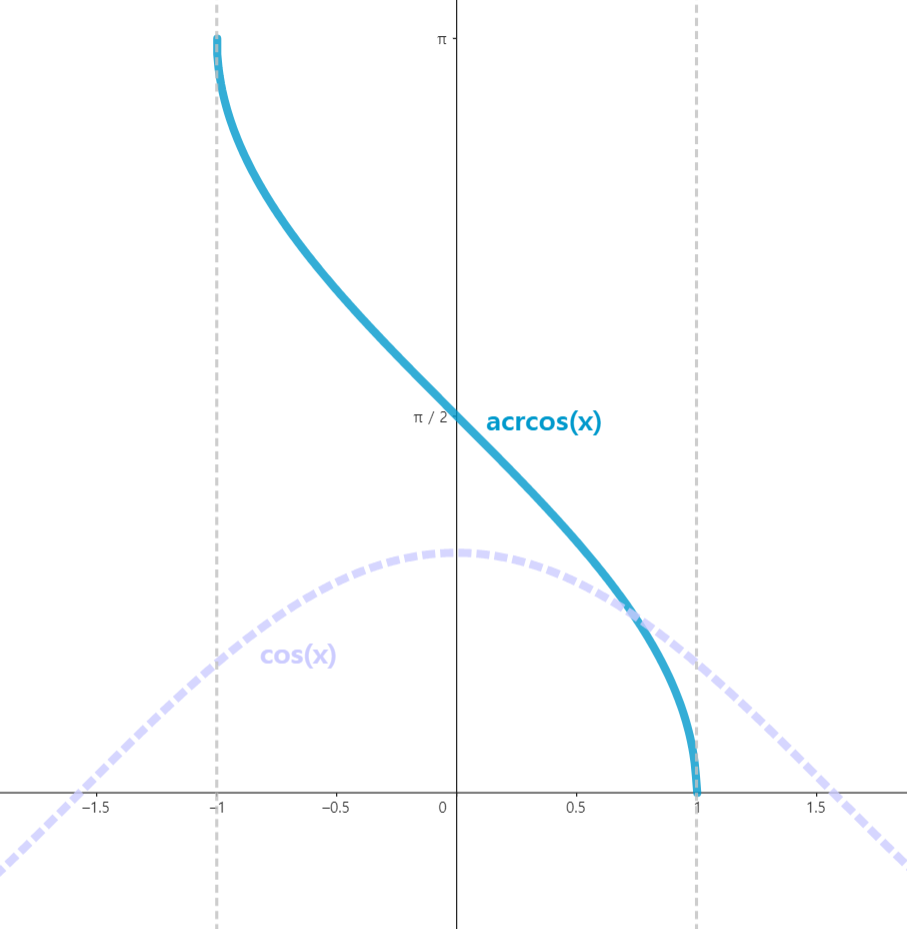
cos의 역함수는 정의역 $0^\circ$, $180^\circ$ 공역-1,1 로 제한을 하여 역삼수를 만들 수 있으며 이를 arccos 함수 라고한다.
tan 함수는 $-90^\circ$, $90^\circ$일때의 y값이 존재하지 않으므로 전단사함수가 되기위해 정의역 구간을 $-90^\circ$, $90^\circ$을 제외한 ( $-90^\circ$, $90^\circ$ ) 범위가 되어야한다.
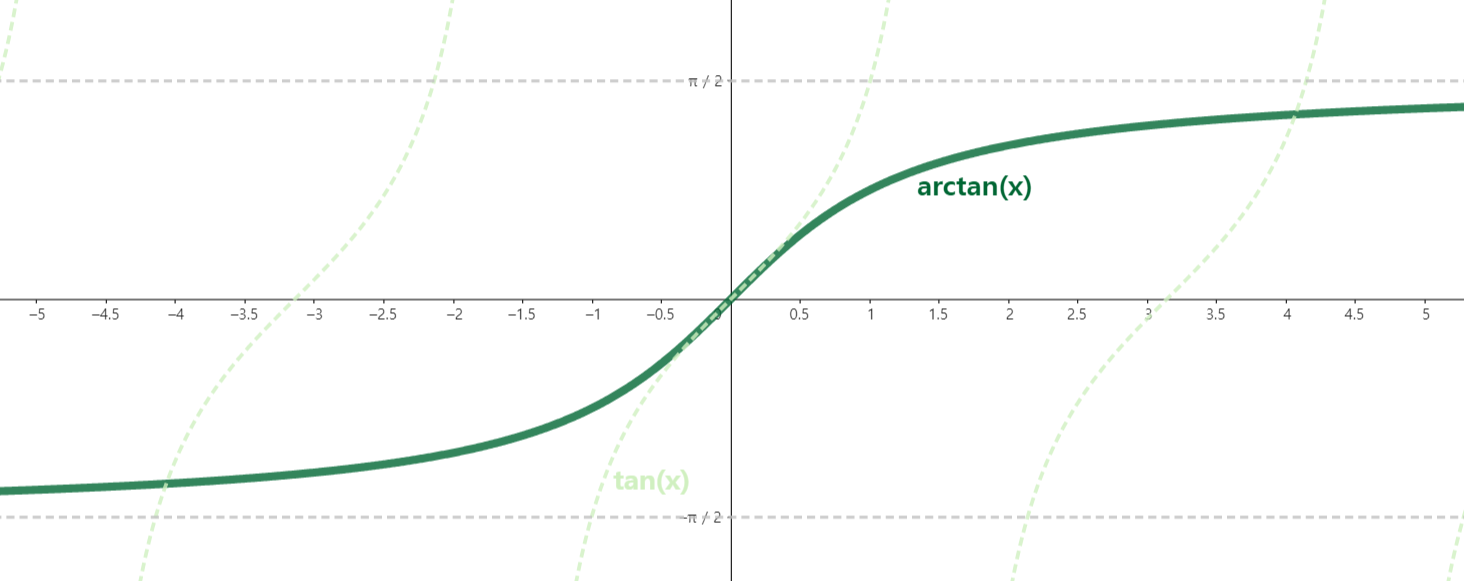
이를 arctan 함수는 벡터의 각도를 구하는데 유용하게 사용된다.
임의의 벡터 (x,y)를 분수식$y\over x$ 을 계산하면 벡터로 두어 tan 함수 값을 얻을 수 있는데 이 값을 arctan 에 넣으면 해당벡터가 x 축과 이루는 사잇각을 얻을 수 있다.
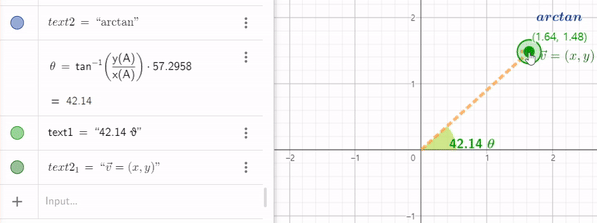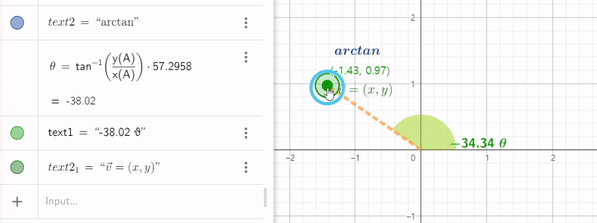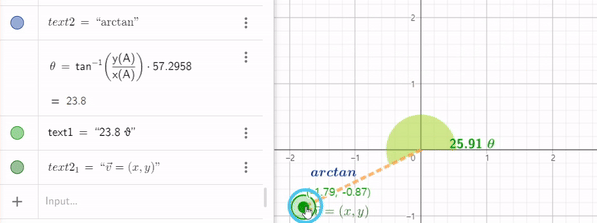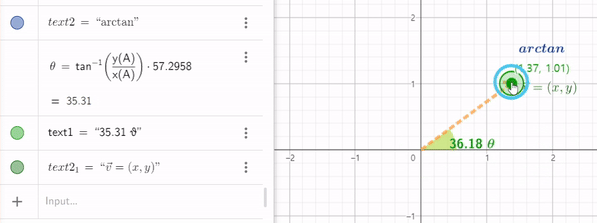
그러나 3 사분면에서는 x,y 값이 둘다 음수가 되어 $x\over y$ 분수 값이 양수가 되기 때문에 1사분면에 해당하는 각의 정보가 나와버린다. x와 y값을 따로 전달하여 모든 사분면에 대응하는 값을 얻는 함수가 있는데 이를 atan2 함수라고 부른다.

atan2 함수의 그래프는 공역이 ($-180 ^\circ$ ,$180 ^\circ$ ) 범위를 가진다.
4.4 극좌표계

데카르트 좌표계로 회전을 구현할때는 x와y의 변화를 매번 계산해야 해서 번거로운 반면 극좌표계는 회전 동작을 기반을 설계된 좌표계기 때문에 회전을 구현하기 편리하다.
극좌표계는 원점으로 부터의거리 $r$ 와 각도 $theta$ 로 구성된다.
벡터를 극좌표계 $(r,\theta)$ 로 변환하기
$r= \sqrt{x^2+y^2}$
$\theta =atan2(y)x$
극좌표계 $(r,\theta)$를 데카르트 좌표계$(x,y)$로 변환하기
$x = r\cdot cos\theta$
$y = r\cdot sin\theta$
'study > math' 카테고리의 다른 글
| [이득우 게임수학] 행렬의 설계 (0) | 2024.06.26 |
|---|---|
| [이득우 게임수학] 행렬 (0) | 2024.06.17 |
| [이득우 게임수학] 선형성과 선형변환 (0) | 2024.06.09 |
| [이득우 게임수학] 벡터 (0) | 2024.05.16 |
| [이득우 게임수학] 수 (0) | 2024.05.13 |




댓글